Note
Go to the end to download the full example code.
Multiple-kernel ridge path between two kernels¶
This example demonstrates the path of all possible ratios of kernel weights between two kernels, in a multiple kernel ridge regression model. Over the path of ratios, the kernels are weighted by the kernel weights, then summed, and a joint model is fit on the obtained kernel. The explained variance on a test set is then computed, and decomposed over both kernels.
from functools import partial
import numpy as np
import matplotlib.pyplot as plt
from himalaya.backend import set_backend
from himalaya.kernel_ridge import MultipleKernelRidgeCV
from himalaya.kernel_ridge import Kernelizer
from himalaya.kernel_ridge import ColumnKernelizer
from himalaya.progress_bar import bar
from himalaya.utils import generate_multikernel_dataset
from sklearn.pipeline import make_pipeline
from sklearn import set_config
set_config(display='diagram')
In this example, we use the cupy backend.
backend = set_backend("cupy", on_error="warn")
/home/runner/work/himalaya/himalaya/himalaya/backend/_utils.py:66: UserWarning: Setting backend to cupy failed: Cupy not installed..Falling back to numpy backend.
warnings.warn(f"Setting backend to {backend} failed: {str(error)}."
Generate a random dataset¶
X_train : array of shape (n_samples_train, n_features)
X_test : array of shape (n_samples_test, n_features)
Y_train : array of shape (n_samples_train, n_targets)
Y_test : array of shape (n_samples_test, n_targets)
n_targets = 50
kernel_weights = np.tile(np.array([0.6, 0.4])[None], (n_targets, 1))
(X_train, X_test, Y_train, Y_test,
kernel_weights, n_features_list) = generate_multikernel_dataset(
n_kernels=2, n_targets=n_targets, n_samples_train=600,
n_samples_test=300, random_state=42, noise=0.31,
kernel_weights=kernel_weights)
feature_names = [f"Feature space {ii}" for ii in range(len(n_features_list))]
Create a MultipleKernelRidgeCV model, see plot_mkr_sklearn_api.py for more details.
# Find the start and end of each feature space X in Xs.
start_and_end = np.concatenate([[0], np.cumsum(n_features_list)])
slices = [
slice(start, end)
for start, end in zip(start_and_end[:-1], start_and_end[1:])
]
# Create a different ``Kernelizer`` for each feature space.
kernelizers = [(name, Kernelizer(), slice_)
for name, slice_ in zip(feature_names, slices)]
column_kernelizer = ColumnKernelizer(kernelizers)
# Create a MultipleKernelRidgeCV model.
solver_params = dict(alphas=np.logspace(-5, 5, 41), progress_bar=False)
model = MultipleKernelRidgeCV(kernels="precomputed", solver="random_search",
solver_params=solver_params,
random_state=42)
pipe = make_pipeline(column_kernelizer, model)
pipe
Then, we manually perform a hyperparameter grid search for the kernel weights.
# Make the score method use `split=True` by default.
model.score = partial(model.score, split=True)
# Define the hyperparameter grid search.
ratios = np.logspace(-4, 4, 41)
candidates = np.array([1 - ratios / (1 + ratios), ratios / (1 + ratios)]).T
# Loop over hyperparameter candidates
split_r2_scores = []
for candidate in bar(candidates, "Hyperparameter candidates"):
# test one hyperparameter candidate at a time
pipe[-1].solver_params["n_iter"] = candidate[None]
pipe.fit(X_train, Y_train)
# split the R2 score between both kernels
scores = pipe.score(X_test, Y_test)
split_r2_scores.append(backend.to_numpy(scores))
# average scores over targets for plotting
split_r2_scores_avg = np.array(split_r2_scores).mean(axis=2)
[ ] 0% | 0.00 sec | Hyperparameter candidates |
[ ] 2% | 1.29 sec | Hyperparameter candidates | 0.77 it/s, ETA: 00:00:51
[. ] 5% | 2.63 sec | Hyperparameter candidates | 0.76 it/s, ETA: 00:00:51
[.. ] 7% | 3.89 sec | Hyperparameter candidates | 0.77 it/s, ETA: 00:00:49
[.. ] 10% | 5.29 sec | Hyperparameter candidates | 0.76 it/s, ETA: 00:00:48
[... ] 12% | 6.58 sec | Hyperparameter candidates | 0.76 it/s, ETA: 00:00:47
[.... ] 15% | 7.96 sec | Hyperparameter candidates | 0.75 it/s, ETA: 00:00:46
[..... ] 17% | 9.34 sec | Hyperparameter candidates | 0.75 it/s, ETA: 00:00:45
[..... ] 20% | 10.73 sec | Hyperparameter candidates | 0.75 it/s, ETA: 00:00:44
[...... ] 22% | 12.18 sec | Hyperparameter candidates | 0.74 it/s, ETA: 00:00:43
[....... ] 24% | 13.52 sec | Hyperparameter candidates | 0.74 it/s, ETA: 00:00:41
[........ ] 27% | 15.00 sec | Hyperparameter candidates | 0.73 it/s, ETA: 00:00:40
[........ ] 29% | 16.43 sec | Hyperparameter candidates | 0.73 it/s, ETA: 00:00:39
[......... ] 32% | 17.46 sec | Hyperparameter candidates | 0.74 it/s, ETA: 00:00:37
[.......... ] 34% | 18.61 sec | Hyperparameter candidates | 0.75 it/s, ETA: 00:00:35
[.......... ] 37% | 20.10 sec | Hyperparameter candidates | 0.75 it/s, ETA: 00:00:34
[........... ] 39% | 21.53 sec | Hyperparameter candidates | 0.74 it/s, ETA: 00:00:33
[............ ] 41% | 22.76 sec | Hyperparameter candidates | 0.75 it/s, ETA: 00:00:32
[............. ] 44% | 24.15 sec | Hyperparameter candidates | 0.75 it/s, ETA: 00:00:30
[............. ] 46% | 25.45 sec | Hyperparameter candidates | 0.75 it/s, ETA: 00:00:29
[.............. ] 49% | 26.89 sec | Hyperparameter candidates | 0.74 it/s, ETA: 00:00:28
[............... ] 51% | 28.31 sec | Hyperparameter candidates | 0.74 it/s, ETA: 00:00:26
[................ ] 54% | 29.76 sec | Hyperparameter candidates | 0.74 it/s, ETA: 00:00:25
[................ ] 56% | 31.09 sec | Hyperparameter candidates | 0.74 it/s, ETA: 00:00:24
[................. ] 59% | 32.50 sec | Hyperparameter candidates | 0.74 it/s, ETA: 00:00:23
[.................. ] 61% | 33.84 sec | Hyperparameter candidates | 0.74 it/s, ETA: 00:00:21
[................... ] 63% | 35.29 sec | Hyperparameter candidates | 0.74 it/s, ETA: 00:00:20
[................... ] 66% | 36.66 sec | Hyperparameter candidates | 0.74 it/s, ETA: 00:00:19
[.................... ] 68% | 38.01 sec | Hyperparameter candidates | 0.74 it/s, ETA: 00:00:17
[..................... ] 71% | 39.31 sec | Hyperparameter candidates | 0.74 it/s, ETA: 00:00:16
[..................... ] 73% | 40.77 sec | Hyperparameter candidates | 0.74 it/s, ETA: 00:00:14
[...................... ] 76% | 41.86 sec | Hyperparameter candidates | 0.74 it/s, ETA: 00:00:13
[....................... ] 78% | 43.27 sec | Hyperparameter candidates | 0.74 it/s, ETA: 00:00:12
[........................ ] 80% | 44.67 sec | Hyperparameter candidates | 0.74 it/s, ETA: 00:00:10
[........................ ] 83% | 46.01 sec | Hyperparameter candidates | 0.74 it/s, ETA: 00:00:09
[......................... ] 85% | 47.52 sec | Hyperparameter candidates | 0.74 it/s, ETA: 00:00:08
[.......................... ] 88% | 48.76 sec | Hyperparameter candidates | 0.74 it/s, ETA: 00:00:06
[........................... ] 90% | 50.23 sec | Hyperparameter candidates | 0.74 it/s, ETA: 00:00:05
[........................... ] 93% | 51.48 sec | Hyperparameter candidates | 0.74 it/s, ETA: 00:00:04
[............................ ] 95% | 52.93 sec | Hyperparameter candidates | 0.74 it/s, ETA: 00:00:02
[............................. ] 98% | 54.22 sec | Hyperparameter candidates | 0.74 it/s, ETA: 00:00:01
[..............................] 100% | 55.53 sec | Hyperparameter candidates | 0.74 it/s, ETA: 00:00:00
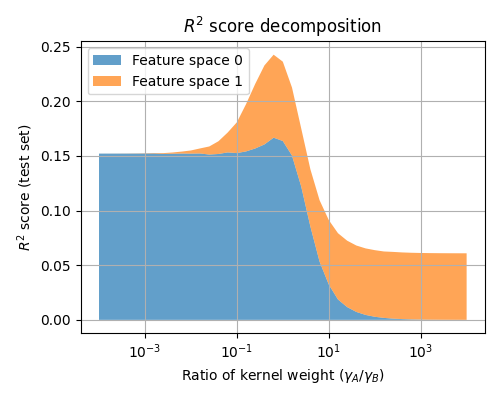
Plot the variance decomposition for all the hyperparameter ratios.
For a ratio of 1e-3, feature space 0 is almost not used. For a ratio of 1e3, feature space 1 is almost not used. The best ratio is here around 1, because the feature spaces are used with similar scales in the simulated dataset.
fig, ax = plt.subplots(figsize=(5, 4))
accumulator = np.zeros_like(ratios)
for split in split_r2_scores_avg.T:
ax.fill_between(ratios, accumulator, accumulator + split, alpha=0.7)
accumulator += split
ax.set(xscale='log')
ax.set(xlabel=r"Ratio of kernel weight ($\gamma_A / \gamma_B$)")
ax.set(ylabel=r"$R^2$ score (test set)")
ax.set(title=r"$R^2$ score decomposition")
ax.legend(feature_names, loc="upper left")
ax.grid()
fig.tight_layout()
plt.show()
Total running time of the script: (0 minutes 55.950 seconds)