Multiple-kernel ridge refining

This example demonstrates how to solve multiple-kernel ridge regression with hyperparameter random search, then refine the results with hyperparameter gradient descent.

import numpy as np

from himalaya.backend import set_backend
from himalaya.kernel_ridge import MultipleKernelRidgeCV
from himalaya.kernel_ridge import Kernelizer
from himalaya.kernel_ridge import ColumnKernelizer
from himalaya.utils import generate_multikernel_dataset

from sklearn.pipeline import make_pipeline
from sklearn import set_config
set_config(display='diagram')

In this example, we use the cupy backend (GPU).

backend = set_backend("cupy", on_error="warn")

/home/runner/work/himalaya/himalaya/himalaya/backend/_utils.py:55: UserWarning: Setting backend to cupy failed: Cupy not installed..Falling back to numpy backend.
  warnings.warn(f"Setting backend to {backend} failed: {str(error)}."

Generate a random dataset

• X_train : array of shape (n_samples_train, n_features)

• X_test : array of shape (n_samples_test, n_features)

• Y_train : array of shape (n_samples_train, n_targets)

• Y_test : array of shape (n_samples_test, n_targets)

(X_train, X_test, Y_train, Y_test, kernel_weights,
 n_features_list) = generate_multikernel_dataset(n_kernels=4, n_targets=50,
                                                 n_samples_train=600,
                                                 n_samples_test=300,
                                                 random_state=42)

feature_names = [f"Feature space {ii}" for ii in range(len(n_features_list))]

Prepare the pipeline

# Find the start and end of each feature space X in Xs
start_and_end = np.concatenate([[0], np.cumsum(n_features_list)])
slices = [
    slice(start, end)
    for start, end in zip(start_and_end[:-1], start_and_end[1:])
]

# Create a different ``Kernelizer`` for each feature space.
kernelizers = [("space %d" % ii, Kernelizer(), slice_)
               for ii, slice_ in enumerate(slices)]
column_kernelizer = ColumnKernelizer(kernelizers)

Define the random-search model

We use very few iteration on purpose, to make the random search suboptimal, and refine it with hyperparameter gradient descent.

solver_params = dict(n_iter=5, alphas=np.logspace(-10, 10, 41))

model_1 = MultipleKernelRidgeCV(kernels="precomputed", solver="random_search",
                                solver_params=solver_params, random_state=42)
pipe_1 = make_pipeline(column_kernelizer, model_1)

# Fit the model on all targets
pipe_1.fit(X_train, Y_train)

[                              ] 0% | 0.00 sec | 5 random sampling with cv |
[......                        ] 20% | 1.32 sec | 5 random sampling with cv | 0.75 it/s, ETA: 00:00:05
[............                  ] 40% | 2.85 sec | 5 random sampling with cv | 0.70 it/s, ETA: 00:00:04
[..................            ] 60% | 4.27 sec | 5 random sampling with cv | 0.70 it/s, ETA: 00:00:02
[........................      ] 80% | 5.69 sec | 5 random sampling with cv | 0.70 it/s, ETA: 00:00:01
[..............................] 100% | 7.07 sec | 5 random sampling with cv | 0.71 it/s, ETA: 00:00:00

Pipeline(steps=[('columnkernelizer',
                 ColumnKernelizer(transformers=[('space 0', Kernelizer(),
                                                 slice(np.int64(0), np.int64(1000), None)),
                                                ('space 1', Kernelizer(),
                                                 slice(np.int64(1000), np.int64(2000), None)),
                                                ('space 2', Kernelizer(),
                                                 slice(np.int64(2000), np.int64(3000), None)),
                                                ('space 3', Kernelizer(),
                                                 slice(np.int64(3000), np.int64(4000), None))])),
                ('multiplekernelrid...
       1.00000000e-02, 3.16227766e-02, 1.00000000e-01, 3.16227766e-01,
       1.00000000e+00, 3.16227766e+00, 1.00000000e+01, 3.16227766e+01,
       1.00000000e+02, 3.16227766e+02, 1.00000000e+03, 3.16227766e+03,
       1.00000000e+04, 3.16227766e+04, 1.00000000e+05, 3.16227766e+05,
       1.00000000e+06, 3.16227766e+06, 1.00000000e+07, 3.16227766e+07,
       1.00000000e+08, 3.16227766e+08, 1.00000000e+09, 3.16227766e+09,
       1.00000000e+10]),
                                                      'n_iter': 5}))])

In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.

Define the gradient-descent model

solver_params = dict(max_iter=10, hyper_gradient_method="direct",
                     max_iter_inner_hyper=10,
                     initial_deltas="here_will_go_the_previous_deltas")

model_2 = MultipleKernelRidgeCV(kernels="precomputed", solver="hyper_gradient",
                                solver_params=solver_params)
pipe_2 = make_pipeline(column_kernelizer, model_2)

Use the random-search to initialize the gradient-descent

# We might want to refine only the best predicting targets, since the
# hyperparameter gradient descent is less efficient over many targets.
top = 60  # top 60%
best_cv_scores = backend.to_numpy(pipe_1[-1].cv_scores_.max(0))
mask = best_cv_scores > np.percentile(best_cv_scores, 100 - top)

pipe_2[-1].solver_params['initial_deltas'] = pipe_1[-1].deltas_[:, mask]
pipe_2.fit(X_train, Y_train[:, mask])

[                              ] 0% | 0.00 sec | hypergradient_direct |
[                              ] 0% | 0.00 sec | hypergradient_direct |
[...                           ] 10% | 3.20 sec | hypergradient_direct | 0.31 it/s, ETA: 00:00:28
[......                        ] 20% | 3.92 sec | hypergradient_direct | 0.51 it/s, ETA: 00:00:15
[.........                     ] 30% | 4.67 sec | hypergradient_direct | 0.64 it/s, ETA: 00:00:10
[............                  ] 40% | 5.41 sec | hypergradient_direct | 0.74 it/s, ETA: 00:00:08
[...............               ] 50% | 6.15 sec | hypergradient_direct | 0.81 it/s, ETA: 00:00:06
[..................            ] 60% | 6.89 sec | hypergradient_direct | 0.87 it/s, ETA: 00:00:04
[.....................         ] 70% | 7.63 sec | hypergradient_direct | 0.92 it/s, ETA: 00:00:03
[........................      ] 80% | 8.37 sec | hypergradient_direct | 0.96 it/s, ETA: 00:00:02
[...........................   ] 90% | 9.10 sec | hypergradient_direct | 0.99 it/s, ETA: 00:00:01
[..............................] 100% | 9.89 sec | hypergradient_direct | 1.01 it/s, ETA: 00:00:00

Pipeline(steps=[('columnkernelizer',
                 ColumnKernelizer(transformers=[('space 0', Kernelizer(),
                                                 slice(np.int64(0), np.int64(1000), None)),
                                                ('space 1', Kernelizer(),
                                                 slice(np.int64(1000), np.int64(2000), None)),
                                                ('space 2', Kernelizer(),
                                                 slice(np.int64(2000), np.int64(3000), None)),
                                                ('space 3', Kernelizer(),
                                                 slice(np.int64(3000), np.int64(4000), None))])),
                ('multiplekernelrid...
       [ 21.57146  , -19.856195 ,  -6.040684 ,  20.622723 , -21.007488 ,
         -5.857005 ,   7.958505 ,  -7.008298 ,  20.622723 ,   7.958505 ,
        -19.856195 ,  -4.9082675,  10.058536 ,   8.907243 ,  10.126631 ,
         21.639557 , -13.180669 , -21.007488 , -14.331962 ,  -7.008298 ,
          8.907243 ,   7.958505 ,  21.57146  , -13.180669 ,   7.958505 ,
          7.7559505,  15.601645 ,  -4.9082675,  21.57146  ,  21.57146  ]],
      dtype=float32),
                                                      'max_iter': 10,
                                                      'max_iter_inner_hyper': 10}))])

In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.

Compute predictions on a test set

import matplotlib.pyplot as plt

# use the first model for all targets
test_scores_1 = pipe_1.score(X_test, Y_test)

# use the second model for the refined targets
test_scores_2 = backend.copy(test_scores_1)
test_scores_2[mask] = pipe_2.score(X_test, Y_test[:, mask])

test_scores_1 = backend.to_numpy(test_scores_1)
test_scores_2 = backend.to_numpy(test_scores_2)
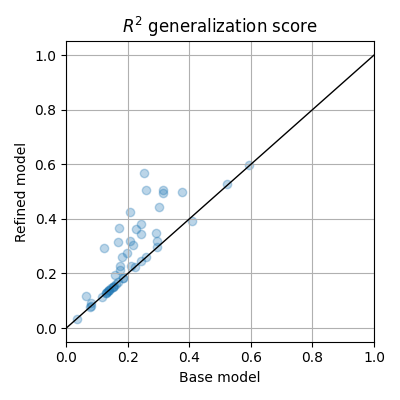
plt.figure(figsize=(4, 4))
plt.scatter(test_scores_1, test_scores_2, alpha=0.3)
plt.xlim(0, 1)
plt.plot(plt.xlim(), plt.xlim(), color='k', lw=1)
plt.xlabel(r"Base model")
plt.ylabel(r"Refined model")
plt.title("$R^2$ generalization score")
plt.grid()
plt.tight_layout()
plt.show()