Note
Go to the end to download the full example code.
Spatial components of the motion energy filters
This example shows the spatial components of the spatio-temporal filters used
in motion energy features. It does not show the temporal components, since this
gallery does not support animation. To visualize the filters with their
temporal components, you can use moten.viz.plot_3dgabor().
Here we demonstrate how the spatial filters vary in term of spatial
frequencies, locations, and directions.
First, let’s define a motion energy pyramid, using MotionEnergyPyramid.
It defines a set of spatio-temporal Gabor filters.
import moten
pyramid = moten.pyramids.MotionEnergyPyramid(stimulus_vhsize=(300, 400),
stimulus_fps=25)
Then, we define a plotting function, to show the spatial part of these spatio-temporal Gabor filters.
import matplotlib.pyplot as plt # noqa
def plot_spatial_gabors(pyramid, indices):
"""Plot the two quadrature spatial components of a list of Gabor filters.
Note this only show the spatial components of the spatio-temporal filters.
Parameters
----------
pyramid : moten.pyramid.MotionEnergyPyramid instance
indices : list of int
"""
vdim = pyramid.definition['vdim']
size = 0.6
fig, axs = plt.subplots(
2, len(indices), figsize=((len(indices) * 4.25 + 0.25) * size,
7.5 * size), squeeze=False,
sharex=True, sharey=True)
axs.T[0][0].set_ylabel('spatial Gabor (cos)')
axs.T[0][1].set_ylabel('spatial Gabor (sin)')
for ii, axs_ in zip(indices, axs.T):
spatial_sin, spatial_cos = pyramid.get_filter_spatial_quadrature(ii)
axs_[0].imshow(spatial_cos, aspect='equal')
axs_[1].imshow(spatial_sin, aspect='equal')
axs_[0].set_title('filter %d' % ii)
gabor = pyramid.filters[ii]
for ax in axs_:
ax.scatter(gabor['centerh'] * vdim, gabor['centerv'] * vdim,
color='k', marker='+')
ax.set_xticks([])
ax.set_yticks([])
plt.tight_layout()
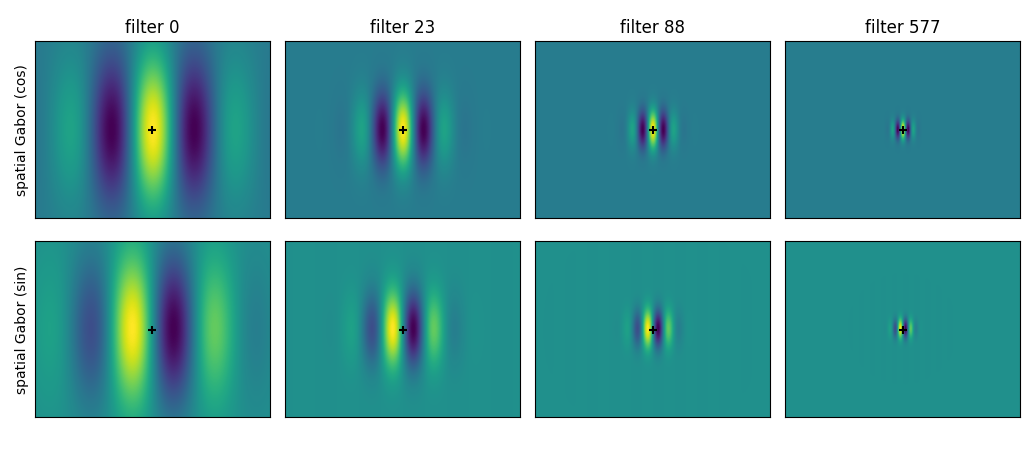
Different spatial frequencies
plot_spatial_gabors(pyramid, [0, 23, 88, 577])
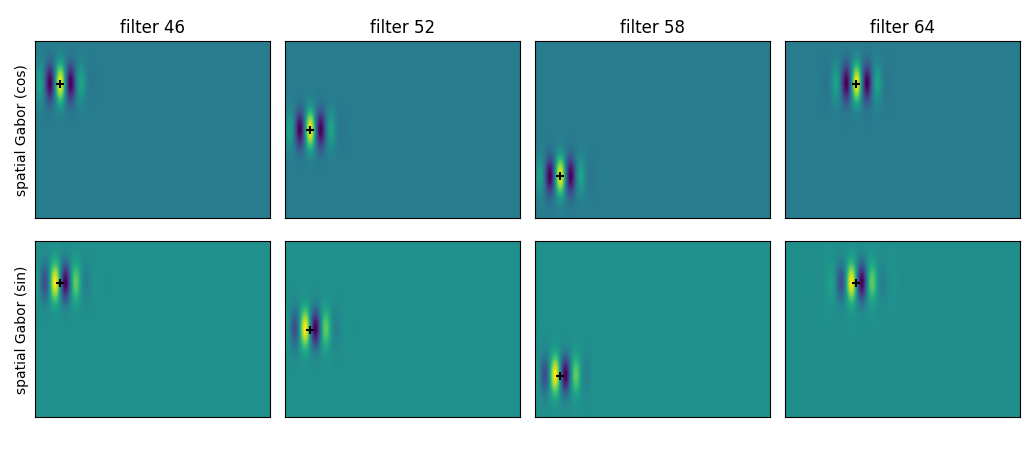
Different locations
plot_spatial_gabors(pyramid, [46, 52, 58, 64])
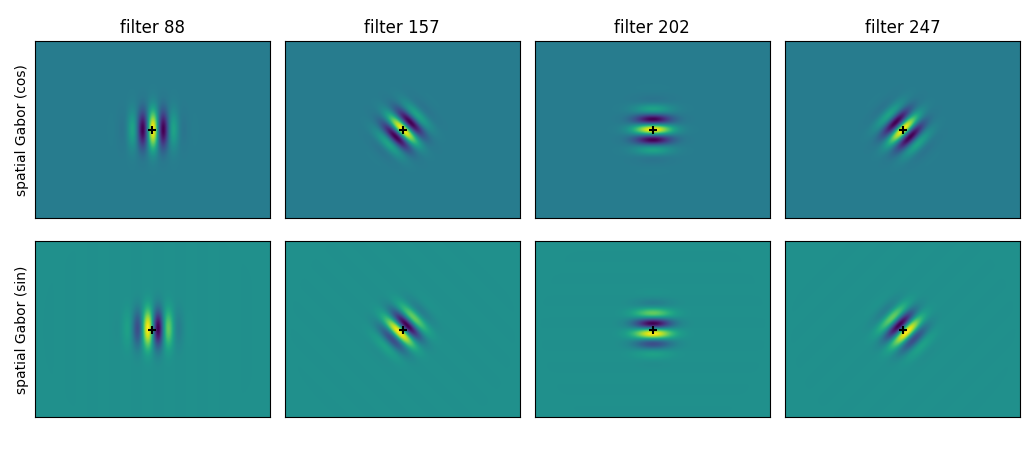
Different directions
plot_spatial_gabors(pyramid, [88, 157, 202, 247])
Total running time of the script: (0 minutes 0.984 seconds)