Note
Go to the end to download the full example code
Visualize the hemodynamic response¶
In this example, we describe how the hemodynamic response function was estimated in the previous model. We fit the same ridge model as in the previous example, and further describe the need to delay the features in time to account for the delayed BOLD response.
Because of the temporal dynamics of neurovascular coupling, the recorded BOLD signal is delayed in time with respect to the stimulus. To account for this lag, we fit encoding models on delayed features. In this way, the linear regression model weighs each delayed feature separately and recovers the shape of the hemodynamic response function in each voxel separately. In turn, this method (also known as a Finite Impulse Response model, or FIR) maximizes the model prediction accuracy. With a repetition time of 2 seconds, we typically use 4 delays [1, 2, 3, 4] to cover the peak of the the hemodynamic response function. However, the optimal number of delays can vary depending on the experiment and the brain area of interest, so you should experiment with different delays.
In this example, we show that a model without delays performs far worse than a model with delays. We also show how to visualize the estimated hemodynamic response function (HRF) from a model with delays.
Path of the data directory¶
from voxelwise_tutorials.io import get_data_home
directory = get_data_home(dataset="shortclips")
print(directory)
/home/jlg/mvdoc/voxelwise_tutorials_data/shortclips
# modify to use another subject
subject = "S01"
Load the data¶
We first load the fMRI responses.
import os
import numpy as np
from voxelwise_tutorials.io import load_hdf5_array
file_name = os.path.join(directory, "responses", f"{subject}_responses.hdf")
Y_train = load_hdf5_array(file_name, key="Y_train")
Y_test = load_hdf5_array(file_name, key="Y_test")
print("(n_samples_train, n_voxels) =", Y_train.shape)
print("(n_repeats, n_samples_test, n_voxels) =", Y_test.shape)
(n_samples_train, n_voxels) = (3600, 84038)
(n_repeats, n_samples_test, n_voxels) = (10, 270, 84038)
We average the test repeats, to remove the non-repeatable part of fMRI responses.
Y_test = Y_test.mean(0)
print("(n_samples_test, n_voxels) =", Y_test.shape)
(n_samples_test, n_voxels) = (270, 84038)
We fill potential NaN (not-a-number) values with zeros.
Y_train = np.nan_to_num(Y_train)
Y_test = np.nan_to_num(Y_test)
Then, we load the semantic “wordnet” features.
feature_space = "wordnet"
file_name = os.path.join(directory, "features", f"{feature_space}.hdf")
X_train = load_hdf5_array(file_name, key="X_train")
X_test = load_hdf5_array(file_name, key="X_test")
print("(n_samples_train, n_features) =", X_train.shape)
print("(n_samples_test, n_features) =", X_test.shape)
(n_samples_train, n_features) = (3600, 1705)
(n_samples_test, n_features) = (270, 1705)
Define the cross-validation scheme¶
We define the same leave-one-run-out cross-validation split as in the previous example.
from sklearn.model_selection import check_cv
from voxelwise_tutorials.utils import generate_leave_one_run_out
# indice of first sample of each run
run_onsets = load_hdf5_array(file_name, key="run_onsets")
print(run_onsets)
[ 0 300 600 900 1200 1500 1800 2100 2400 2700 3000 3300]
We define a cross-validation splitter, compatible with scikit-learn API.
n_samples_train = X_train.shape[0]
cv = generate_leave_one_run_out(n_samples_train, run_onsets)
cv = check_cv(cv) # copy the cross-validation splitter into a reusable list
Define the model¶
We define the same model as in the previous example. See the previous example for more details about the model definition.
from sklearn.pipeline import make_pipeline
from sklearn.preprocessing import StandardScaler
from voxelwise_tutorials.delayer import Delayer
from himalaya.kernel_ridge import KernelRidgeCV
from himalaya.ridge import RidgeCV
from himalaya.backend import set_backend
backend = set_backend("torch_cuda", on_error="warn")
X_train = X_train.astype("float32")
X_test = X_test.astype("float32")
alphas = np.logspace(1, 20, 20)
pipeline = make_pipeline(
StandardScaler(with_mean=True, with_std=False),
Delayer(delays=[1, 2, 3, 4]),
KernelRidgeCV(
alphas=alphas, cv=cv,
solver_params=dict(n_targets_batch=500, n_alphas_batch=5,
n_targets_batch_refit=100)),
)
from sklearn import set_config
set_config(display='diagram') # requires scikit-learn 0.23
pipeline
Fit the model¶
We fit on the train set, and score on the test set.
pipeline.fit(X_train, Y_train)
scores = pipeline.score(X_test, Y_test)
scores = backend.to_numpy(scores)
print("(n_voxels,) =", scores.shape)
(n_voxels,) = (84038,)
Intermission: understanding delays¶
To have an intuitive understanding of what we accomplish by delaying the
features before model fitting, we will simulate one voxel and a single
feature. We will then create a Delayer object (which was used in the
previous pipeline) and visualize its effect on our single feature. Let’s
start by simulating the data.
# number of total trs
n_trs = 50
# repetition time for the simulated data
TR = 2.0
rng = np.random.RandomState(42)
y = rng.randn(n_trs)
x = np.zeros(n_trs)
# add some arbitrary value to our feature
x[15:20] = .5
x += rng.randn(n_trs) * 0.1 # add some noise
# create a delayer object and delay the features
delayer = Delayer(delays=[0, 1, 2, 3, 4])
x_delayed = delayer.fit_transform(x[:, None])
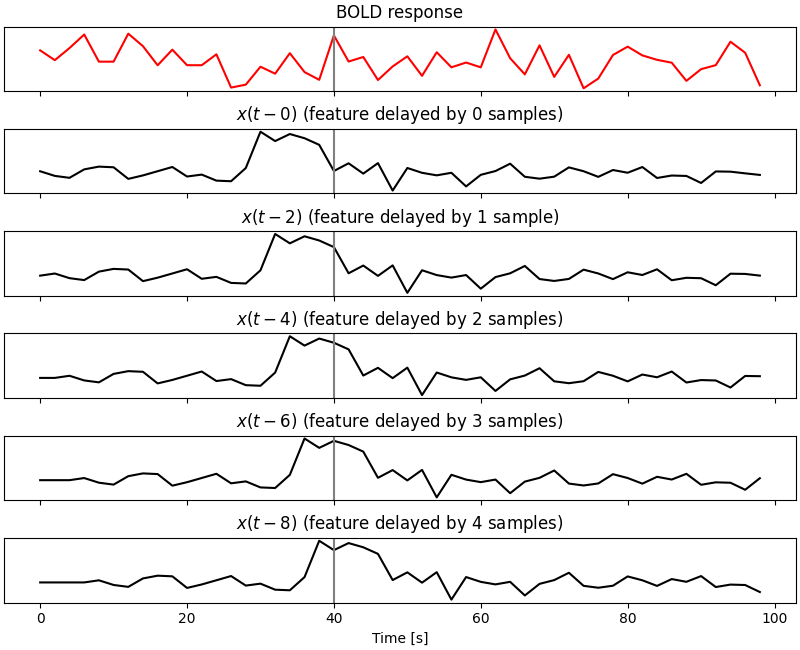
In the next cell we are plotting six lines. The subplot at the top shows the simulated BOLD response, while the other subplots show the simulated feature at different delays. The effect of the delayer is clear: it creates multiple copies of the original feature shifted forward in time by how many samples we requested (in this case, from 0 to 4 samples, which correspond to 0, 2, 4, 6, and 8 s in time with a 2 s TR).
When these delayed features are used to fit a voxelwise encoding model, the brain response \(y\) at time \(t\) is simultaneously modeled by the feature \(x\) at times \(t-0, t-2, t-4, t-6, t-8\). In the remaining of this example we will see that this method improves model prediction accuracy and it allows to account for the underlying shape of the hemodynamic response function.
import matplotlib.pyplot as plt
fig, axs = plt.subplots(6, 1, figsize=(8, 6.5), constrained_layout=True,
sharex=True)
times = np.arange(n_trs) * TR
axs[0].plot(times, y, color="r")
axs[0].set_title("BOLD response")
for i, (ax, xx) in enumerate(zip(axs.flat[1:], x_delayed.T)):
ax.plot(times, xx, color='k')
ax.set_title("$x(t - {0:.0f})$ (feature delayed by {1} sample{2})".format(
i * TR, i, "" if i == 1 else "s"))
for ax in axs.flat:
ax.axvline(40, color='gray')
ax.set_yticks([])
_ = axs[-1].set_xlabel("Time [s]")
plt.show()
Compare with a model without delays¶
We define here another model without feature delays (i.e. no Delayer).
Because the BOLD signal is inherently slow due to the dynamics of
neuro-vascular coupling, this model is unlikely to perform well.
Note that if we remove the feature delays, we will have more fMRI samples (3600) than number of features (1705). In this case, running a kernel version of ridge regression is computationally suboptimal. Thus, to create a model without delays we are using RidgeCV instead of KernelRidgeCV.
pipeline_no_delay = make_pipeline(
StandardScaler(with_mean=True, with_std=False),
RidgeCV(
alphas=alphas, cv=cv, solver="svd",
solver_params=dict(n_targets_batch=500, n_alphas_batch=5,
n_targets_batch_refit=100)),
)
pipeline_no_delay
We fit and score the model as the previous one.
pipeline_no_delay.fit(X_train, Y_train)
scores_no_delay = pipeline_no_delay.score(X_test, Y_test)
scores_no_delay = backend.to_numpy(scores_no_delay)
print("(n_voxels,) =", scores_no_delay.shape)
(n_voxels,) = (84038,)
Then, we plot the comparison of model prediction accuracies with a 2D histogram. All ~70k voxels are represented in this histogram, where the diagonal corresponds to identical prediction accuracy for both models. A distribution deviating from the diagonal means that one model has better prediction accuracy than the other.
from voxelwise_tutorials.viz import plot_hist2d
ax = plot_hist2d(scores_no_delay, scores)
ax.set(
title='Generalization R2 scores',
xlabel='model without delays',
ylabel='model with delays',
)
plt.show()
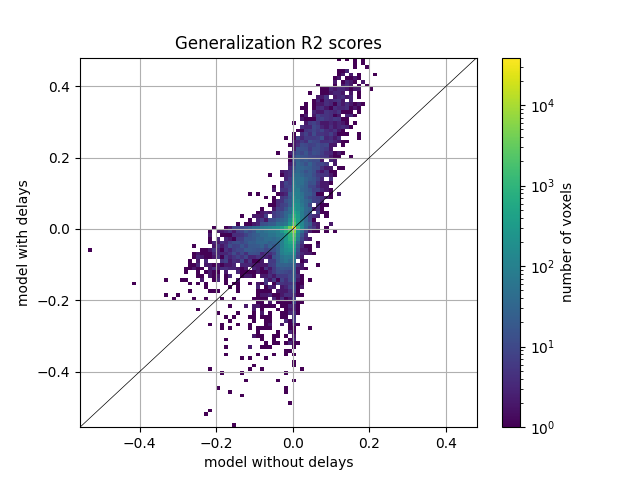
We see that the model with delays performs much better than the model without delays. This can be seen in voxels with scores above 0. The distribution of scores below zero is not very informative, since it corresponds to voxels with poor predictive performance anyway, and it only shows which model is overfitting the most.
Visualize the HRF¶
We just saw that delays are necessary to model BOLD responses. Here we show how the fitted ridge regression weights follow the hemodynamic response function (HRF).
Fitting a kernel ridge regression results in a set of coefficients called the “dual” coefficients \(w\). These coefficients differ from the “primal” coefficients \(\beta\) obtained with a ridge regression, but the primal coefficients can be computed from the dual coefficients using the training features \(X\):
To better visualize the HRF, we will refit a model with more delays, but only on a selection of voxels to speed up the computations.
# pick the 10 best voxels
voxel_selection = np.argsort(scores)[-10:]
# define a pipeline with more delays
pipeline_more_delays = make_pipeline(
StandardScaler(with_mean=True, with_std=False),
Delayer(delays=[0, 1, 2, 3, 4, 5, 6]),
KernelRidgeCV(
alphas=alphas, cv=cv,
solver_params=dict(n_targets_batch=500, n_alphas_batch=5,
n_targets_batch_refit=100)),
)
pipeline_more_delays.fit(X_train, Y_train[:, voxel_selection])
# get the (primal) ridge regression coefficients
primal_coef = pipeline_more_delays[-1].get_primal_coef()
primal_coef = backend.to_numpy(primal_coef)
# split the ridge coefficients per delays
delayer = pipeline_more_delays.named_steps['delayer']
primal_coef_per_delay = delayer.reshape_by_delays(primal_coef, axis=0)
print("(n_delays, n_features, n_voxels) =", primal_coef_per_delay.shape)
# select the feature with the largest coefficients for each voxel
feature_selection = np.argmax(np.sum(np.abs(primal_coef_per_delay), axis=0),
axis=0)
primal_coef_selection = primal_coef_per_delay[:, feature_selection,
np.arange(len(voxel_selection))]
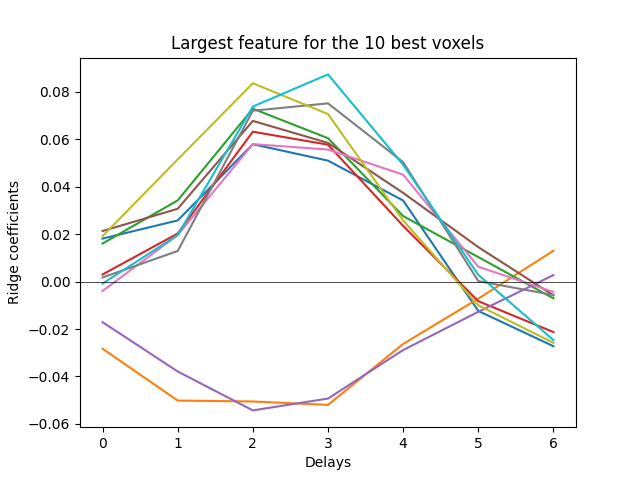
plt.plot(delayer.delays, primal_coef_selection)
plt.xlabel('Delays')
plt.xticks(delayer.delays)
plt.ylabel('Ridge coefficients')
plt.title(f'Largest feature for the {len(voxel_selection)} best voxels')
plt.axhline(0, color='k', linewidth=0.5)
plt.show()
(n_delays, n_features, n_voxels) = (7, 1705, 10)
We see that the hemodynamic response function (HRF) is captured in the model weights. Note that in this dataset, the brain responses are recorded every two seconds.
Total running time of the script: (0 minutes 57.648 seconds)